Вы видите ночной вариант оформления страницы.
кликните здесь, чтобы увидеть дневной!

Вы видите ночной вариант оформления страницы.
кликните здесь, чтобы увидеть дневной!

Москва
«Наука», Главная редакция физико-математической литературы
1973
448 с.
| Страница | строка | напечатано | следует читать |
|---|---|---|---|
| 19 | 6 сн. | разбиение 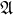 | разбиение 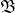 |
| 33 | 7 сн. | к поятию | к понятию |
| > | 5 сн. | павило, | правило, |
| 142 | 20 сн. | (1821—1845) | (1821—1895) |
| 144 | 8 сн. | (1)φ = 1 | (1)ψ = 1 |
| > | 7 сн. | (n)φ = 1 | (n)ψ = 1 |
| 145 | 1 сн. | 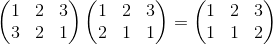 |
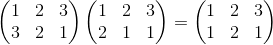 |
| 146 | 6 св. | (y)φ)ψ | ((y)φ)ψ |
| 151 | 1 св. | il → il−1 для l+1 < k | il → il+1 для l+1 ≤ k |
| 158 | 13 св. и следующие | в определении 5 | в определении 7 |
| 159 | 6 св. | на множестве M | на множестве M′ |
| 161 | 8 сн. | ((g1 g2 ... gm)(gm+1gm+2 ... gn−1))g | ((g1g2 ... gm)(gm+1gm+2 ... gn−1))gn |
| 166 | 20 и 15 сн. | (G, M) | (G, M′) |
| 171 | Таблица 1, строка β | β α2β αβ ε α α2 | β α2β αβ ε α2α |
| 175 | 3 св. | Ось BF:(12)(03) | Ось BF(02)(13) |
| > | 4 св. | Ось CD:(02)(13) | Ось CD:(12)(03) |
| 176 | 9 св. | (0321)·(4405) | (0321)·(4765) |
| > | 12 св. | ·(17)·(36) | ·(27)·(36) |
| 179 | 19 сн. | называемых | называемые |
| 184 | 2 и 4 св. | R+ | R(+) |
| > | 6 сн. | (1)·πg = g | (1)πg = g |
| > | 6—5 сн. | (1)·πg′ = g′ | (1)πg′ = g′ |
| 187 | 20 св. | (G2, M) | (G2, M′ |
| 188 | 3—5 св. | 1 4 3 2 ↓ a b c d | 1 4 3 2 ↓ a d c b |
| 191 | 1 сн. | H+g1H+g2H+...+gk+1H | H+g1H+g2H+...+gk−1H |
| 199 | 11 св. | предложению 4, Exp (G) < (G:1) | предложению 6, Exp (G) ≤ (G:1) |
| 205 | 14 сн. | (K g1)φ (K g2)φ | (K g1)φˆ (K g2)φˆ |
| 206 | 13 св. | (h1g1)−1g1−1h1−1 = h1−1g | (h1g1)−1 = g1−1h1−1 = h1−1g* |
| 212 | 14 сн. | {g1, 1(G1)), g1 ∈ G} | {(g1, 1(G2)), g1 ∈ G1} |
| > | 12 сн. | (1(G2), g2) | (1(G1), g2) |
| 213 | 3 и 9 св. | G1, G2 | Ĝ1Ĝ2 |
| 213 | 12 св. | (g1, 1)(1, gn) | (g1, 1)(1, g2) |
| 214 | 6 св. | h1(h2h1−1h2) | h1(h2h1−1h2−1) |
| > | 19 св. | g′1−1g1 = g′2 g2−1 | |
| 217 | (16) | 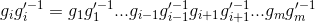 |
 |
| 232 | 4 св. | g: x → xg | ĝ: x → xg |
| 234 | 2 св. | (n1, n1,...,nk) | (n1, n2,...,nk) |
| > | 4 св. | условия | условие |
| > | 2 сн. | левых классов | правых классов |
| 235 | 12 св. | (G, 1) = |N| | (G:1) =|N| |
| 237 | 8 св. | состоящее | состоящих |
| > | 17 сн. | n(n−1)(n−2)...(n−k−1) | n(n−1)(n−2)...(n−k+1) [или: n(n-1)(n-2)...(n-(k-1))] |
| 239 | 2 св. | изоморфной | изоморфный |
| 243 | колонтитул | рпимеры | примеры |
| 431 | 3 св. | (a·b = b·c) | (a·b = b·a) |
| 431 | 19 сн. | с правым, левым | с левым, правым |
| 434 | 18 св. | (a∧b = b∧c) | (a∧b = b∧a) |
Мы не можем не отметить здесь ряд
дидактических достоинств изложения, к которым относится в том числе использование Автором
коммутативных диаграмм.
Известно, что с дидактической точки зрения основные теоретико-групповые понятия
целесообразно вводить на материале теории групп преобразований. Этому принципу следует и Л. А. Калужнин.
Особенно удачным у Автора следует признать введение понятия сопряженности элементов группы,
которое возникает как обобщение «подобия» подстановок.
Заметим, однако, что при этом Автор не вводит термина "сопряженные подгруппы" и кладет
в основу определения инвариантной подгруппы тождество левого и правого разложений, а не инвариантность
относительно внутренних автоморфизмов; с нашей точки зрения этот второй вариант определения несколько сложнее,
но удобнее в употреблении и, что ещё важнее, лучше отражает сущность вводимого объекта.
Стр. 208. Термин «слово над множеством»
заимствован из теории свободных групп, основной метод которой — отвлечение от природы элементов
группы путём перехода к их именам; употребление его здесь кажется нам излишним.
Стр. 232. Странно, что термин «центр группы» появляется здесь без прямого определения
(отметим: Z(G) = Ker (^) =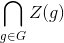
= {h | ∀g∈G: g−1hg = h} = {h | ∀g∈G: h−1gh = g} = {h|∀g∈G: gh = hg} etc.)
Предложение 6 §5 не имеет прямого отношения к содержанию параграфа, но есть немедленное следствие предложения 4 §6, где его и следовало бы сформулировать.
Автор обозначает разные объекты 1(G) и E = {1(G)} одним символом, что может привести к недоразумениям.
Это же неразличение заложено в распространенном обозначении порядка G через "(G : 1)".
В скором времени я выложу сюда ответы и решения к задачам.

Третье издание.
М., "Наука",
1967
648 с.
Первое издание книги вышло в 1945 году (рецензию на это изд. можно найти здесь),
второе — в 1953
(рецензия).
В 2005 г. издательство «Лань»
выпустило четвертое, стереотипное издание.
| Страница | Строка | Напечатано | Должно быть |
|---|---|---|---|
| 30 | 6 св. | aβ aγ = aα | aβ aγ = aβ |
| 70 | 18 св. | трасформирование | трансформирование |
| 96 | (3) | C = | G = |
| 434 | 4 св. | сосле | после |
Вероятно, многие из вас изучали теорию групп именно по этой книге, ставшей классической,
успевшей устареть, но сохранившей свою образовательную ценность и поныне.
Скорее всего, при чтении книги вы находили неточности и опечатки; мы предлагаем
сообщить нам о них (и тем самым облегчить жизнь будущим читателям), заполнив форму
ниже!
18 сентября 2019 года пользователь se прислал нам следующее
сообщение: Также se сообщил, что владеет богатым материалом,
но, к сожалению, не может нам сейчас его передать. Большое спасибо Вам за Ваше сообщение! Пожалуйста, пишите ещё! ✉смотреть
Список опечаток к книге Л. А. Калужнина "Введение в общую алгебру".
Последняя опечатка (стр 434). Я долго сравнивал, но мне кажется то, что справа (следует читать) идентично тому, что слева.
Мне нравится простой спокойный дизайн.
то, что справа, идентично тому, что слева.
se, Вы совершенно правы, это мое упущение (ошибка уже исправлена; для других посетителей поясним,
что в первоначальном варианте в ячейке "следует читать" стояло «(a∧b = b∧c)»).Мне нравится простой спокойный дизайн.
Спасибо! Сам разрабатывал :)
Взошла на горы чорна тень! Перед Вами ночной дизайн страницы.
Когда Солнце взойдет, оно осветит эту страничку.