Добрый вечер!
Кликните здесь, чтобы увидеть дневную страницу!

Добрый вечер!
Кликните здесь, чтобы увидеть дневную страницу!

Москва
«Высшая школа»,1988
(В 1981 вышло первое издание в двух томах.)
| Страница | Строка | Напечатано | Следует читать |
|---|---|---|---|
| 33 | Формула 1.16 | 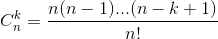 |
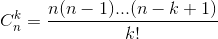 |
| 58 | Формула 2.17 | 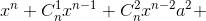 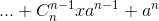 |
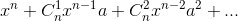
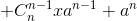 |
| 93 | 8—9 св. | одна из бесконечностей ∞, +∞ или ∞ | одна из бесконечностей ∞, +∞ или −∞ |
| 167 | 7 сн. | 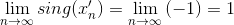 |
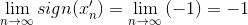 |
| 111 | 5 сн. | | |xn| − |a| | < |xn − a| | | |xn| − |a| | ≤ |xn − a| |
| 115 | 4.1 | 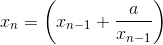 |
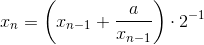 |
| 153 | 1 сн. | 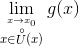 | 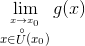 |
| 166 | 17 сн. | −+ | − ∞ |
| 176 | 1 св. | конечно большими | бесконечно большими |
| 179 | 9 сн. | 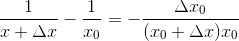 |
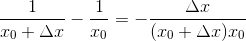 |
| 186 | 22 св. | неравенство | равенство |
| 190 | 13 сн. | g: X → R | g: Y → R |
Заметим, что во вводных главах книги Вы не найдёте упоминаний о лемме Бореля — Лебега. Лемма формулируется гораздо позже, в главах, посвящённых функциям многих переменных.
Между тем, основываясь на лемме, можно предложить новые пути доказательства целого ряда основных теорем о непрерывных функциях: сравните Фихтенгольц, глава II, §5, 89.
Глава I, §5. Определение предела функции.
Отметим два существенных отличия предела в понимании Л. Д. Кудрявцева от предела в определениях других авторов.
Ниже приводим один из вариантов определения Коши в формулировке Л. Д. Кудрявцева:
Точка a называется пределом функции f: X → R при x → x0,
если для любой окрестности U(a) точки a существует такая окрестность U(x0 ) точки x0, что для любой точки
x ∈ X ∩ U(x0 ) выполняется включение f(x) ∈ U(a).
Отсюда видно, что 1) Автор не требует, чтобы x ≠ x0, т. е., не ограничивается проколотой окрестностью x0; и 2) не требует, чтобы
точка x0 была предельной точкой (точкой сгущения по терминологии Г. М. Фихтенгольца), и даже точкой прикосновения множества X.
Таким образом, если мы рассмотрим функцию f, f(0)=1, f(x) = x при x ≠ 0, то увидим, что f не имеет предела в точке 0.
Далее, для множества X = {x ∈ R | x = 0 ∨ |x| ≥ 1} и функции f', f'(0)=1, f'(x) = |x| при x ≠ 0
и даже для множества X = {x ∈ R | |x| ≥ 1} и функции f'', f''(x) = |x| в точке 0 существует предел.
стр. 100
Упражнение 8 (простенькое).
Грубо говоря, нам предлагают доказать,
что всякая последовательность, построенная из всех натуральных чисел, является бесконечно большой.
Моя идея доказательства такова. Для любого a существует ka = sup (k: nk ≤ a). Ясно, что ∀k > ka, nk > a, что и
означает по определению, что предел равен ∞.
стр. 102
примечание 1.
Заметим здесь, что многие авторы используют термин "возрастающая" ("убывающая") последовательность
только в применении к последовательностям, для которых выполнено условие: xn>xn−1 (соответственно, xn<xn−1 ), а "неубывающими" ("невозрастающими") называют
последовательности, являющиеся возрастающими (убывающими) либо стационарными.
стр. 108
Упражнение 12. Условие эквивалентно критерию Коши. Действительно, покажем необходимость; если последовательность сходится, то существует n′?, такое что ∀n, m ≥ n′?, |n−m|≤ ε; положим n? = n′? +1. Достаточность условия следует из неравенства треугольника.
стр. 109
Задача 3. Не следует. Пусть xn = xn−1 + 1/n; как известно, гармонический ряд расходится.
стр. 110
Задача 4. Обобщая понятие суммы для бесконечного числа слагаемых, приходим к понятию ряда;
Достаточно рассмотреть произвольную бесконечно малую последовательность и просуммировать ее
с собой бесконечно много раз. Более интересная задача состоит в построении последовательности
бесконечно малых последовательностей, сумма которой сходится к нулю.
Задача 5. Обозначим через x mn n-ный член m-ной последовательности. Определим n-ную последовательность следующим образом: xn1 =...= xnn-1
=1; xnn = 1/(x n1·x n2·...x nn−1).
Произведение всех построенных таким образом бесконечно малых последовательностей есть стационарная последовательность 1, 1, 1,... .
§5.12, пример 4.
Приведённое Автором доказательство непрерывности функции Римана мы считаем несостоятельным.
§5.16, замечание 4.
Подчеркнём важность условия 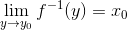 ; нетрудно видеть, что это условие справедливо для любой
непрерывной функции, но в общем случае может не выполняться.
; нетрудно видеть, что это условие справедливо для любой
непрерывной функции, но в общем случае может не выполняться.
Ссылки на страницы изд. 1988 года.
В 4-м, переработанном издании Курса, вышедшем в 2015 году в изд.-ве "Физматлит", исправлена большая часть погрешностей предыдущих изданий. Более того, новое издание более эргономично: книга снабжена колонтитулами, упрощающими поиск формул и теорем, для которых принята система нумерации по главам и параграфам.

М., "Физматлит", 2001 — 2005
"Курс" выдержал множество изданий:
1-е изд.: М. — Л., Гостехиздат; том 1: 1947, т. 2: 1948, т. 3: 1949.
2-е изд.: Гостехиздат, тт. 1, 2: 1948. [?]
3-е изд., исправленное: М. — Л., ГИТТЛ, 1949 — 1951.
4-е изд.: Физматгиз; т. 1: 1958, т. 2: 1959.
5-е изд., стереотипное: М., Физматгиз, 1960 [?].
6-е изд.: М., "Наука"; т. 1 (шестое изд.), т. 2 (шестое изд.), т. 3 (четвертое изд.): 1966
7-е изд., стереотипное: М., "Наука"; т. 1: 1969, т. 2: 1969, т. 3: 1970.
В 1997 году издательство "Лань" выпустило очередное переиздание.
Нам известно о следующих опечатках в тексте первого тома:
С. 67, 3 св.: напечатано: при a > N ; следует: при n > N ;
С. 149, 4 сн.: напечатано: | x | > 1 ; следует: | x | < 1 ;

М, «Физматлит», 2004
| Стр. | Строка | Напечатано: | Следует читать: |
|---|---|---|---|
| 47 | 24 св. | A ∪ B = (A Δ B) ∪ (A ∩ B) | A ∪ B = (A Δ B) Δ (A ∩ B) |
| 49 | 14 сн. | A \ A1 ∈ R | A \ A2 ∈ R |
| 108 | 9 св. | 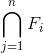 |
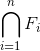 |
| 568 | 14. | Гельфанд Д. А. | Гельфанд И. М. |
Множество A Δ B можно было бы назвать «суммой по модулю 2» множеств A и B.Смысл этого замечания становится вполне ясным, если определить на множестве {0, 1} аддитивную операцию как на множестве классов вычетов по модулю 2. Тогда имеем: IAΔB(x) = IA(x) + IB(x) для любого x. Отсюда видно, что класс всех подмножеств S образует группу относительно Δ, причем ∅ играет роль нейтрального элемента, и для всякого A, A ≠ ∅, Or (A) = 2.

1940
В 1948 году книга вышла вторым изданием,
которое отличалось от первого только
тем, что в нем были исправлены некоторые опечатки.
Поэтому мы рекомендуем Вам
скачать
издание 1948 года и работать с ним.
Если же Вы все же собираетесь читать книгу 1940 года (которая есть
здесь),
то сверяйтесь со списком опечаток, приведенным ниже.
| стр. | строка | напечатано | следует читать |
|---|---|---|---|
| 18 | 2 св. | r≠r | r≠r′ |
| 40 | 4 сн. | K0+K′1+K2′+... | K′0+K1′+K′2+... |
| 42 | 15 св. | 0≤x≤1 | 0≤x1≤1 |
| 44 | |||
| 72 | 4—5 сн. | совершенно нигде неплотного множества | совершенного нигде неплотного множества |
| 79 | 6 св. | E′2 | E2 |
| > | 18 св. | точке ξ | точке ξ1 |
| 81 | 22 сн. | непрерывающихся | неперекрывающихся |
| 105 | 6 сн. | рсссмотрения | рассмотрения |
| 107 | 24 св. | вывод | выбор |
| 108 | 8 сн. | ep′⊰eq′ | ep′⊱eq′ |
| 112 | 15 св. | точки a | точки c |
| 116 | 7 сн. | точке a | точке c |
Последовательность. Под «последовательностью» Автор понимает упорядоченное множество,
не имеющее наибольшего элемента.
Предел последовательности.
Термину «предел последовательности» у Автора в общепринятой терминологии соответствует «частичный
предел последовательности».
↑