Вы видите ночную страничку. Чтобы увидеть, как она выглядит днём, приходите завтра утром! (Или кликните здесь).

Первое издание.
М., "Наука", 1977
| Страница | строка | напечатано | следует читать | ||||
|---|---|---|---|---|---|---|---|
| 42 | 13 ↓ | ∇n | Δn | ||||
| 60 | 17 ↓ |
|
| ||||
| 82 | 13 ↓ | P ∈ K | P ∈ K0 | ||||
| 83 | 15 ↑ | P0 ∈ K0 | Pα ∈ K0 | ||||
| 89 | 28 ↓ | 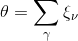 |
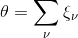 | ||||
| 93 | |||||||
| 93 | 3 ↑ | подмножество | множество | ||||
| 93 | |||||||
| 107 | 6 ↓ | ρ (y, x) | ρ (y, z) | ||||

Издание 2-е, исправленное.
М., МЦНМО, 2012.
Первое издание книги вышло в 2010 году.
3.5, задача 3.7
Здесь имеется в виду известное доказательство Фюрстенберга.
[материал дополняется]
4.5, задачи 4.9 — 4.11.
Очевидно, что если центры шаров совпадают, то условие не выполняется.
Построим метрическое пространство (X, ρ), X = {a, b, c}; ρ : (a, b) → n, (a, c) → n, (b, c) → m,
m ≤ 2n (нетрудно видеть, что ρ удовлетворяет аксиоме треугольника). В этом пространстве для любого l, m > l > n,
Dl (b) ⊂ Dn (a), Dl (b) ≠ Dn (a).
Построенный пример является минимальным в том смысле, что никакое пространство, состоящее менее
чем из трёх точек, не удовлетворяет условию задачи.
§2, упражнение 2.14:
Перечислите все наборы подмножеств трёхэлементного множества, такие, что существуют топологии, в которых эти наборы являются полными наборами замкнутых множеств.
В трёхэлементном множестве X = {a, b, c} существует всего 29 топологий (9 — с точностью до гомеоморфизма). :
| Топология (с точностью до гомеоморфизма): | набор множеств, замкнутых в топологии: | число гомеоморфных топологий: | |
|---|---|---|---|
| Дискретная топология | булеан X (8 подмножеств) | 1 | |
| Антидискретная топология | {X, ∅} | 1 | |
| Топологии, содержащие, кроме X и ∅ | Одноэлементное подмножество; | {X, ∅, {e1, e2}} | 3 |
| Двухэлементное подмножество; | {X, ∅, {e1}} | 3 | |
| Одноэлементное подмножество и его дополнение; | {X, ∅, {e1}, {e2, e3}} | 3 | |
| Два одноэлементных подмножества и их объединение; | {X, ∅, {e1}, {e1, e2}, {e1, e3}} | 3 | |
| Двухэлементное подмножество и его одноэлементное подмножество; | {X, ∅, {e1}, {e1, e2}} | 6 | |
| Два двухэлементных подмножества и их пересечение | {X, ∅, {e1}, {e2}, {e1, e2}} | 3 | |
| Два одноэлементных и два двухэлементных подмножества. | {X, ∅, {e1}, {e3}, {e1, e2}, {e1, e3}} | 6 | |
Между тем, на с. 280 даётся ответ:
Для контроля укажем лишь, что всего существует четырнадцать таких наборов.
Это неверно.

В двух томах.
Перевод М. Я. Антоновского.
Том 1: М., "Мир", 1966. С предисловием П . С. Александрова.